- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct DFA of alternate 0’s and 1’s
Problem
Construct deterministic Finite automata (DFA) whose language consists of strings with alternate 0’s and 1’s over an alphabet ∑ ={0,1}.
Solution
If Σ = {0, 1}
(ε + 1)(01)*
(ε + 0) is the set of strings that alternate 0’s and 1’s
Another expression for the same language is (01)*+ 1(01)*+ (01)*0+ 1(01)*0.
The strings the given language generates are as follows −
If no input is either 0 or 1 then it generates {ε} .
String starts with 0 and followed by 1 = {0101…}.
String starts with 1 followed by 0 ={101010….. }
So, based on string generation it is clear the strings are start with ε,(01)*, (10)*, but there is no restriction that string begin with 0 only or 1 only, so by considering all these points in the mind, the expression that it satisfies the given language with alternate 0’s and 1’s is −
(01)* + (10)* + 0(10)* + 1(01)*
DFA
The DFA for the given language is −
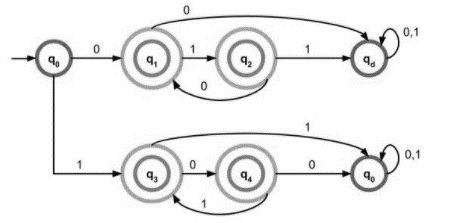
Explanation
Starting with the initial state, the string it generates, q0 on 0 goes to q1 which is one of the final states , accepting only 0, which satisfies the given condition.
Starting with the initial state, the string it generates, q0 on 1 goes to q3 which is one of the final states, accepting only 1, that satisfies the given condition.
q0 to reach final state q2 it generates a string “01” which is accepted by the language.
q0 to reach one of the final states q4, it generates a string “10” which is accepted by the language.
Similarly for the remaining strings also accepted by the DFA.
4K+ Views
