Program to find number of restricted paths from first to last node in Python

Python Server Side Programming Programming

Suppose we have one undirected weighted connected graph. The graph has n nodes and they are labelled from 1 to n. A path from start to end is a sequence of nodes like [z0, z1, z2, ..., zk] here z0 is start node and zk is end node and there is an edge between zi and zi+1 where 0 <= i <= k-1. The distance of a path is the sum of the weights values on the edges of the path. Let dist(x) denotes the shortest distance from node n and node x. A restricted path is a special path that also satisfies that dist(zi) > dist(zi+1) where 0 <= i <= k-1. So, we have to find the number of restricted paths from node 1 to node n. If the answer is too large then return answer modulo 10^9 + 7.

So, if the input is like

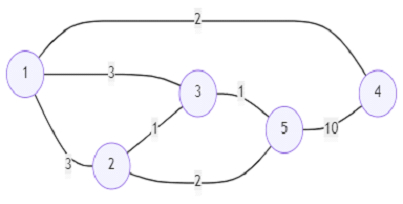
then the output will be 3 because there are three restricted paths (1,2,5), (1,2,3,5), (1,3,5).

To solve this, we will follow these steps −

graph := adjacency list of the graph made from given edge list
paths := an array of size (n+1) and filled with 0
paths[n] := 1
dists := an array of size (n+1) and filled with -1
q := a queue, and insert (0, n) initially
while q is not empty, do
- (dist, node) := front element of q and remove it from q
- if dists[node] is not same as -1, then
  - go for next iteration
- dists[node] := dist
- for each adjacent node v and weight w of graph[node], do
  - if dists[v] is same as -1, then
    - insert (dist + w, v) into q
  - otherwise when dists[v] < dists[node], then
    - paths[node] := paths[node] + paths[v]
- if node is same as 1, then
  - return paths[node] mod 10^9+7
return 0

Example

Let us see the following implementation to get better understanding −

from collections import defaultdict
from heapq import heappop, heappush
def solve(n, edges):
   graph = defaultdict(dict)
   for u, v, w in edges:
      graph[u][v] = w
      graph[v][u] = w

   paths = [0] * (n+1)
   paths[n] = 1
   dists = [-1] * (n+1)
   q = [(0, n)]

   while q:
      dist, node = heappop(q)
      if dists[node] != -1:
         continue

      dists[node] = dist
      for v, w in graph[node].items():
         if dists[v] == -1:
            heappush(q, (dist + w, v))
         elif dists[v] < dists[node]:
            paths[node] += paths[v]

      if node == 1:
         return paths[node] % (10**9 + 7)

   return 0

n = 5
edges = [(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]
print(solve(n, edges))

Input

5,[(1,2,3),(1,3,3),(2,3,1),(1,4,2),(5,2,2),(3,5,1),(5,4,10)]

Output

Arnab Chakraborty

Updated on: 2021-10-06T11:26:05+05:30

259 Views

Kickstart Your Career

Get certified by completing the course

Get Started