What are Precedence Functions in compiler design?

Compiler Design Programming Languages Computer Programming

Precedence relations between any two operators or symbols in the precedence table can be converted to two precedence functions f & g that map terminals symbols to integers.

If a <. b, then f (a) <. g (b)
If a = b, then f (a) =. g (b)
If a .> b, then f (a) .> g (b)

Here a, b represents terminal symbols. f (a) and g (b) represents the precedence functions that have an integer value.

Computations of Precedence Functions

For each terminal a, create the symbol f_a&g_a.
Make a node for each symbol.

If a =. b, then fa & gb are in same group or node.

If a =. b & c =. b, then fa & fc must be in same group or node.

(a) If a <. b, Mark an edge from g_b to f_a.

(b) If a .>b, Mark an edge from f_a to g_b.

If the graph constructed has a cycle, then no precedence functions exist.
If there are no cycles.

(a) f_a = Length of longest path beginning at the group of f_a.

(b) g_a = Length of the longest path from the group of g_a.

Example1 − Construct precedence graph & precedence function for the following table.

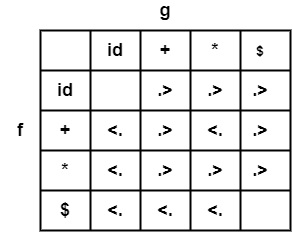
Solution

Step1 − Create Symbols

Step2 − No symbol has equal precedence, as can be seen in the given table; therefore, each symbol will remain in a different node.

Step3 − If a <. b, create an edge from f_a → g_a

If a .>b, create an edge from g_b → f_a

Since, $ <. +,*, id. therefore, make an edge from g₊, g_*, g_id to f_s

Similarity + <. ,∗, id. ∴ make an edge from g_*, g_id to f₊

Similarity * <. id. Therefore, Mark an edge from g_id to f_*.

Since, +,*, id . > $ therefore, Mark an edge from f₊, f_*, f_id to g_s.

Similarity +,*, id . > +. Mark an edge from f₊, f_*, f_id to g₊.

Similarity *, id . > *. Mark an edge from f_*, f_id to g.

Combining all the edges we get

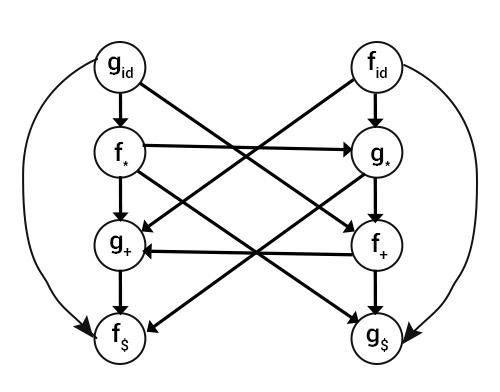
Step4 − Computing the maximum length of the path from each node, we get the following precedence functions

	Id	+	*	$
F	4	2	4	0
G	5	1	3	0

Example2 − Construct precedence graph & precedence function for the following table.

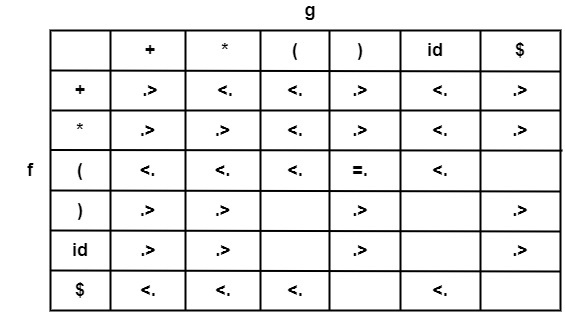
Solution

As we have (=.). Therefore f & g will be in the same group.

Computation of precedence graph

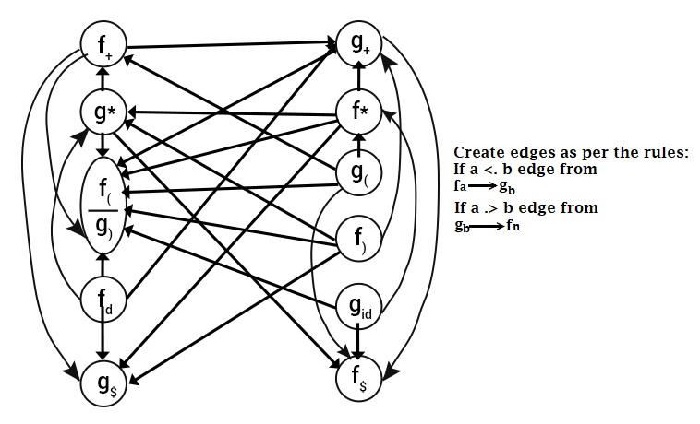
Computation of Precedence Function Table

Since f_$ and g_$ have no outgoing edges, f($ ) = g($ ) = 0.

Since f and g have no outgoing edges, f(( ) = g( )) = 0.

For all others, compute the path of the longest length starting from it.

For Example −

Take f₊,

It has three outgoing edges and traces out its paths.

f₊ → g_$

f₊ → f₍

f₊ → g₊ → f₍ and f₊ → g₊ → f_$

Select the path of maximum length, and the length is 2.

Hence, f₊ = 2. computing all paths of f and g, we get Precedence table

	+	*	(	)	id	$
F	2	4	0	4	4	0
G	1	3	5	0	5	0

Ginni

Updated on: 2021-10-30T12:34:29+05:30

4K+ Views

Kickstart Your Career

Get certified by completing the course

Get Started